密码学 | Cwww3's Blog

哈希

定义

把任意长度的输入通过哈希算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射。散列值又称摘要(Digest)、校验值(Checksum)、指纹(Fingerprint)

用途

完整性校验
加密

具体应用
安全Hash编码法(Secure Hash Algorithm)
- SHA家族的五个算法，分别是SHA-1、SHA-224、SHA-256、SHA-384，和SHA-512，后四者有时并称为SHA-2。
MD5(Standards for Message Digest)
循环冗余校验 CRC-32 (Cyclic redundancy check)

1
2
3

md := md5.New()
md.Write([]byte("msg"))
sum := md.Sum(nil)

安全性

一般来讲，长度越长，安全性越高，计算耗时越长。安全性高的被用作加密，安全性低的主要用来做完整性校验对称加密

对称加密

定义

同一个密钥可以同时用来加密和解密，这种加密方法称为对称加密，也称为单密钥加密

用途

加密

具体应用

DES
- 密钥的长度必须为 8 个字符（64 位）
3DES
- 密钥的长度必须为 24 个字符
AES
- 密钥的长度可以是 16/24/32 个字符（128/192/256 位）。

加密方式

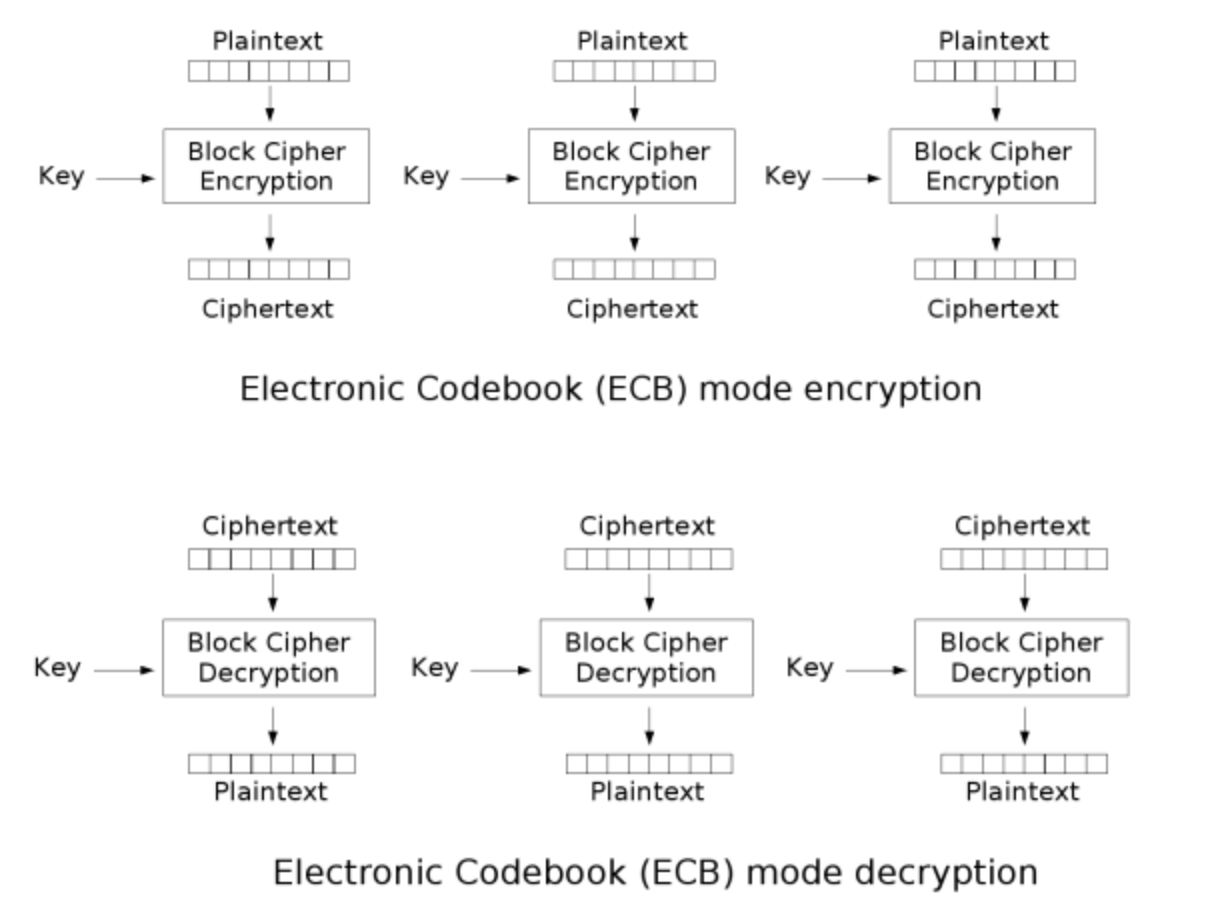
ECB(Electronic codebook) ：把每一个数据块独立加密，最后拼接。解密时先拆分后解密。

填充

数据补位一般有NoPadding和PKCS7Padding(JAVA中是PKCS5Padding)填充方式，PKCS7Padding和PKCS5Padding实际只是协议不一样，根据相关资料说明：PKCS5Padding明确定义了加密块是8字节，PKCS7Padding加密快可以是1-255之间。但是封装的DES算法默认都是8字节，所以可以认为他们一样。数据补位实际是在数据不满8字节的倍数，才补充到8字节的倍数的填充过程。
NoPadding填充方式：算法本身不填充，比如.NET的padding提供了有None，Zeros方式，分别为不填充和填充0的方式。
PKCS7Padding（PKCS5Padding）填充方式：为.NET和JAVA的默认填充方式，对加密数据字节长度对8取余为r，如r大于0，则补8-r个字节，字节为8-r的值；如果r等于0，则补8个字节8。比如：加密字符串为为AAA，则补位为AAA55555;加密字符串为BBBBBB，则补位为BBBBBB22；加密字符串为CCCCCCCC，则补位为CCCCCCCC88888888。

// AEC-ECB
src := []byte("123456")
key := []byte("1234567890123456")
dst , _ := openssl.AesECBEncrypt(src, key, openssl.PKCS7_PADDING)
fmt.Printf(base64.StdEncoding.EncodeToString(dst))  // yXVUkR45PFz0UfpbDB8/ew==

dst , _ = openssl.AesECBDecrypt(dst, key, openssl.PKCS7_PADDING)
fmt.Println(string(dst)) // 123456

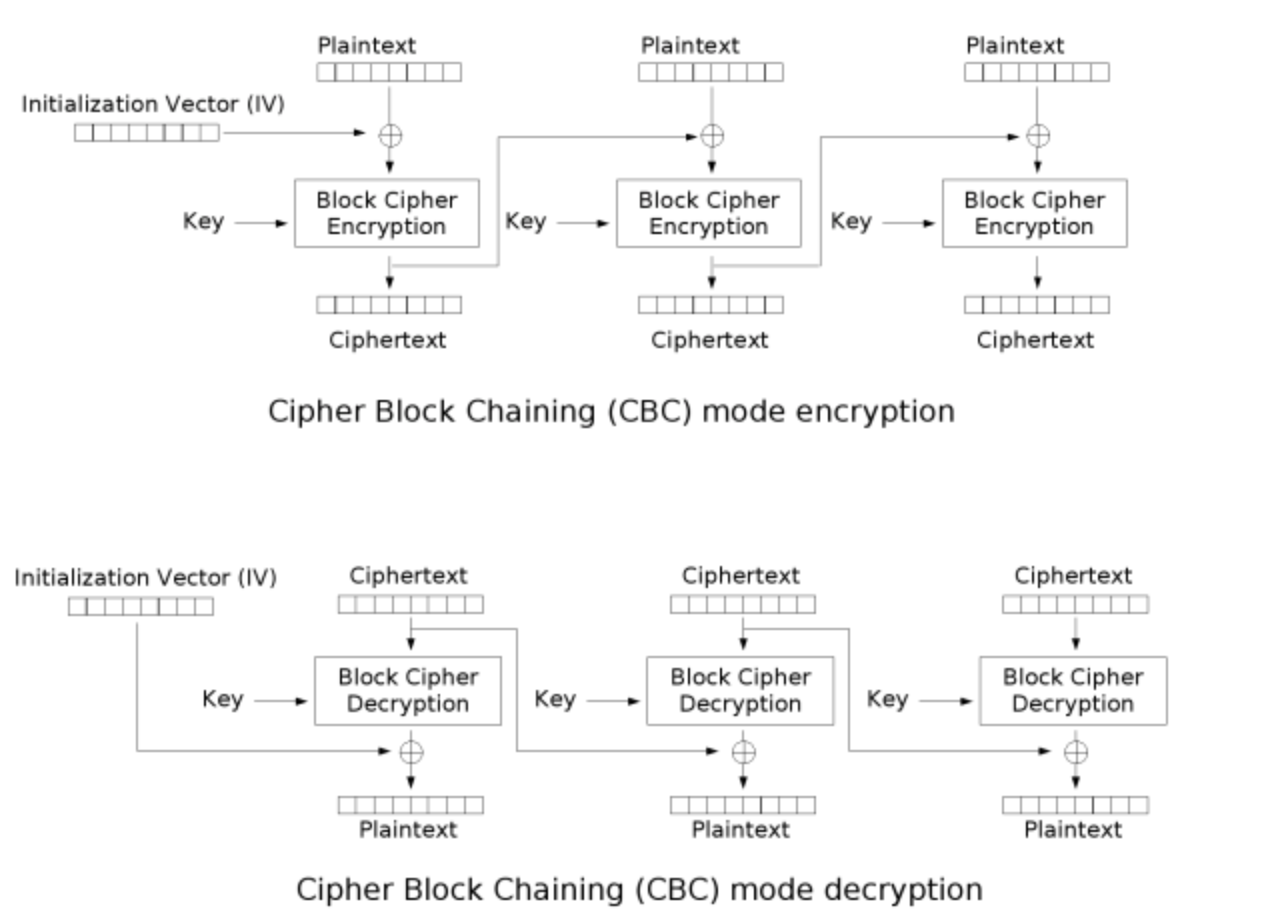
CBC(Cipher-block chaining)：加密每一个数据块时，都会与上一个数据块之间有联系。第一个块中需要使用初始化向量。

// AEC-CBC
src := []byte("123456")
key := []byte("1234567890123456")
iv := []byte("1234567890123456")
dst , _ := openssl.AesCBCEncrypt(src, key, iv, openssl.PKCS7_PADDING)
fmt.Println(base64.StdEncoding.EncodeToString(dst)) // 1jdzWuniG6UMtoa3T6uNLA==

dst , _ = openssl.AesCBCDecrypt(dst, key, iv, openssl.PKCS7_PADDING)
fmt.Println(string(dst)) // 123456

非对称加密

定义

又名公开密钥加密(public-key cryptography) 使用两个不同的密钥：加密密钥和解密密钥。这两个密钥是数学相关，用某用户加密密钥加密后所得的信息，只能用该用户的解密密钥才能解密。如果知道了其中一个，并不能计算出另外一个。因此如果公开了一对密钥中的一个，并不会危害到另外一个的秘密性质。称公开的密钥为公钥；不公开的密钥为私钥。

用途

加密通信(公钥加密，私钥解密)
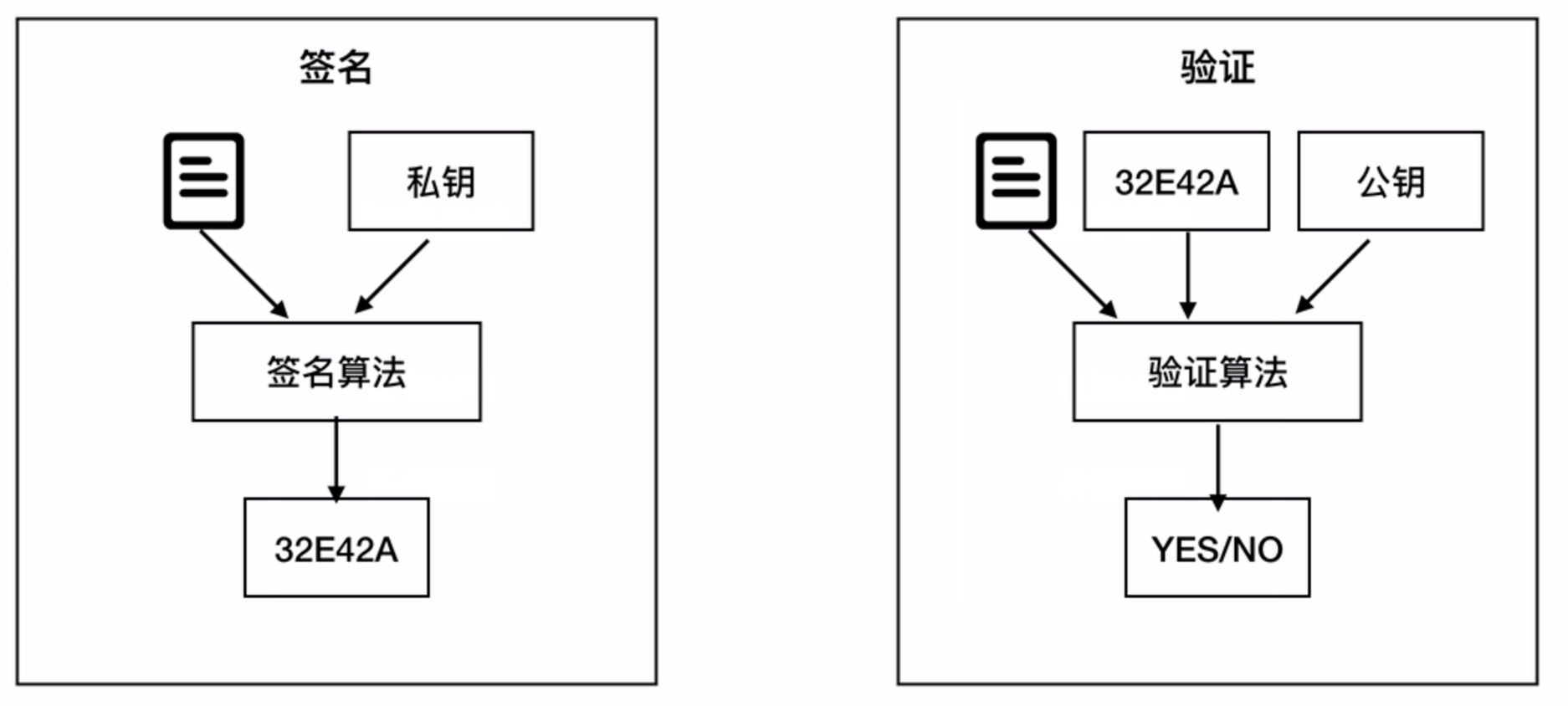
数字签名(私钥加密，公钥解密)
- 认证、防止抵赖、验证完整性

具体应用

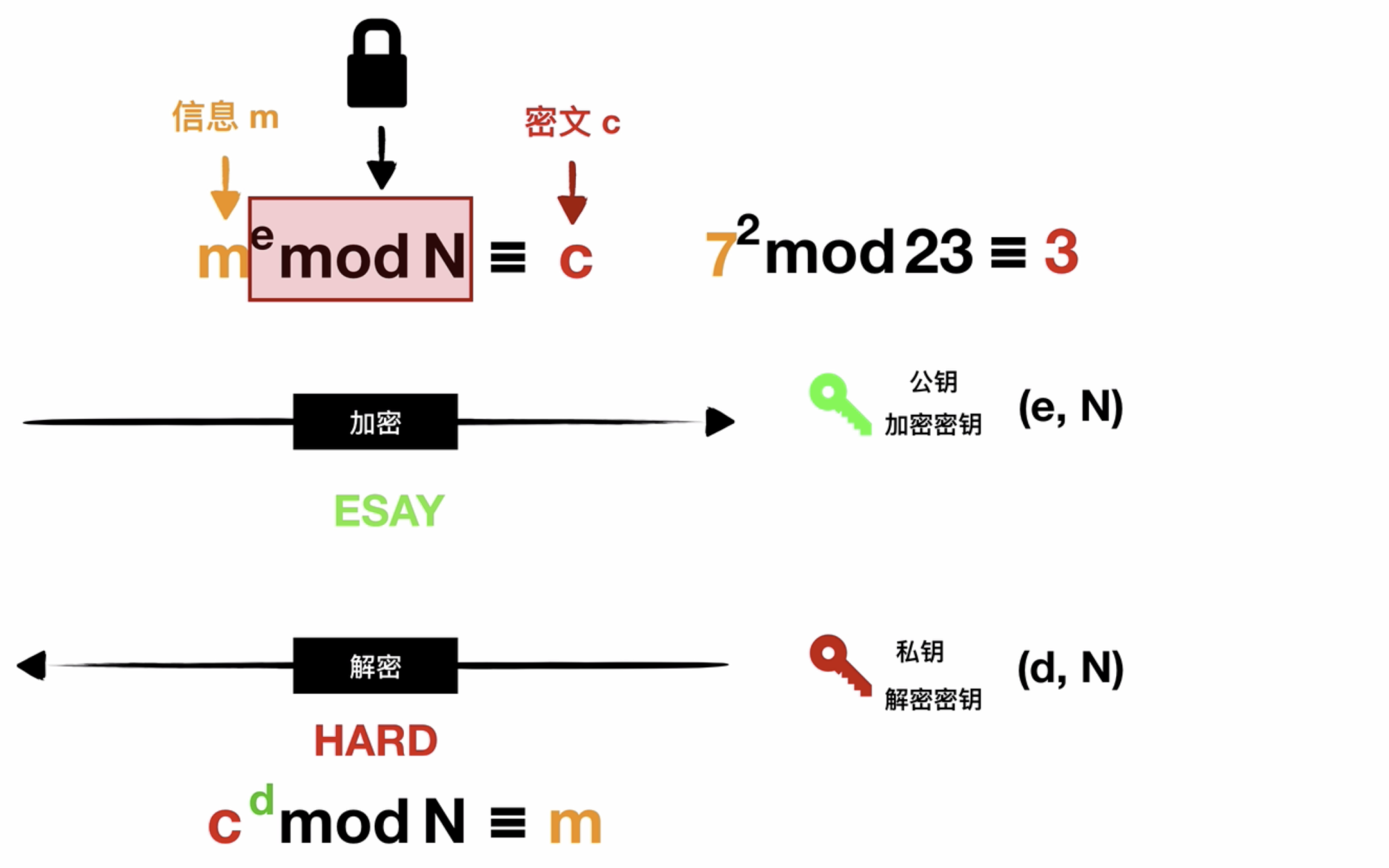
RSA
- 基于整数分解

ECC椭圆曲线算法(效率高)
- 基于离散对数

安全性

根据公钥运算出私钥的难度越大，越安全。

// 生成秘钥对
privateKey, err := rsa.GenerateKey(rand.Reader, 1024)
if err != nil {
   panic(err)
}
// 公钥
publicKey := privateKey.PublicKey
msg := []byte("重要信息")
sha := sha256.New()
// 加密信息
encryptedMsg, err := rsa.EncryptOAEP(sha, rand.Reader, &publicKey, msg, nil)
if err != nil {
   panic(err)
}
fmt.Println(encryptedMsg)
// 解密信息
decryptedMsg, err := privateKey.Decrypt(nil, encryptedMsg, &rsa.OAEPOptions{Hash: crypto.SHA256})
if err != nil {
   panic(err)
}
fmt.Println(string(decryptedMsg))

数字签名

数字签名在发送方，分两步：
1. 从内容算摘要（哈希算法）
2. 从摘要明文到摘要密文，也称数字签名（发送方私钥+加密算法）
数字签名验证在接收方，分两步：
1. 从摘要密文（数字签名）到摘要明文（发送方公钥+解密算法）
2. 从收到的内容当场计算摘要（哈希算法），与（1）的结果比对是否一致
如果一致，可以说明两点：
1. 内容未被篡改（摘要一致）
2. 内容只能是私钥拥方发送，不可抵赖（密文能够用对方的公钥解开）

然后单独想一下，

为什么要对摘要加密后再发送？为什么不直接发摘要？摘要不可以逆向推导原文，摘要泄露了也没事……

答：摘要泄露是没事，但不怀好意的人的目的可能并不在想要窃听你发送了什么，而是想伪造发送的内容让你相信。通过同时替换摘要和内容，很简单就实现了。所以摘要需要经过加密，不怀好意的人没有私钥，无法完成加密。或者说你收到的东西只要能用公钥解密，你才认为这个东西确实是对应私钥持有者完成的。这叫做当事人不可抵赖，同时别人无法仿冒。（数字签名：不可抵赖+无法仿冒）

为什么不直接对内容加密，而是先生成摘要，对摘要加密？

答：可能是内容很长吧，直接加密算半天！摘要算法可以把无限长的内容输出成长度固定的摘要，再进行加密时间就是可以预估的

数字证书(digital certificate)

数字签名很完美，你用公钥能够解密，说明确实是私钥方发送的，你很放心……但有没有想过，万一这把公钥本身，就被人做了手脚？？？ 为了保证“公钥”是可信的，数字证书应运而生。发送方先把自己的公钥给CA，CA用CA的私钥和CA加密算法对其进行加密得到加密后的发送方公钥，用于生成CA的数字证书。
发送时不仅发送内容、数字签名，还包含发送方的数字证书。
接收方拿到后
1. 首先从数字证书中解密出发送方公钥（用的是CA的公钥和CA解密算法），这个公钥必然是可信的。
2. 然后就是和前面一样的流程，拿发送方公钥去解密数字签名，得到摘要；最后比对摘要是否一致。

一个问题：既然数字证书是为了保证发送方公钥不是别人伪造的，那怎么保证“CA”的公钥不是伪造的呢？
答：CA是第三方机构，CA公钥是公开的，接收方可以跟别人比对（比如在网上查询），因此不可能伪造。但是发送方公钥，接收方是通过通信得到的，收到后无法验证。