Cwww3's Blog

Record what you think

0%

背包问题

发表于 更新于 Valine：

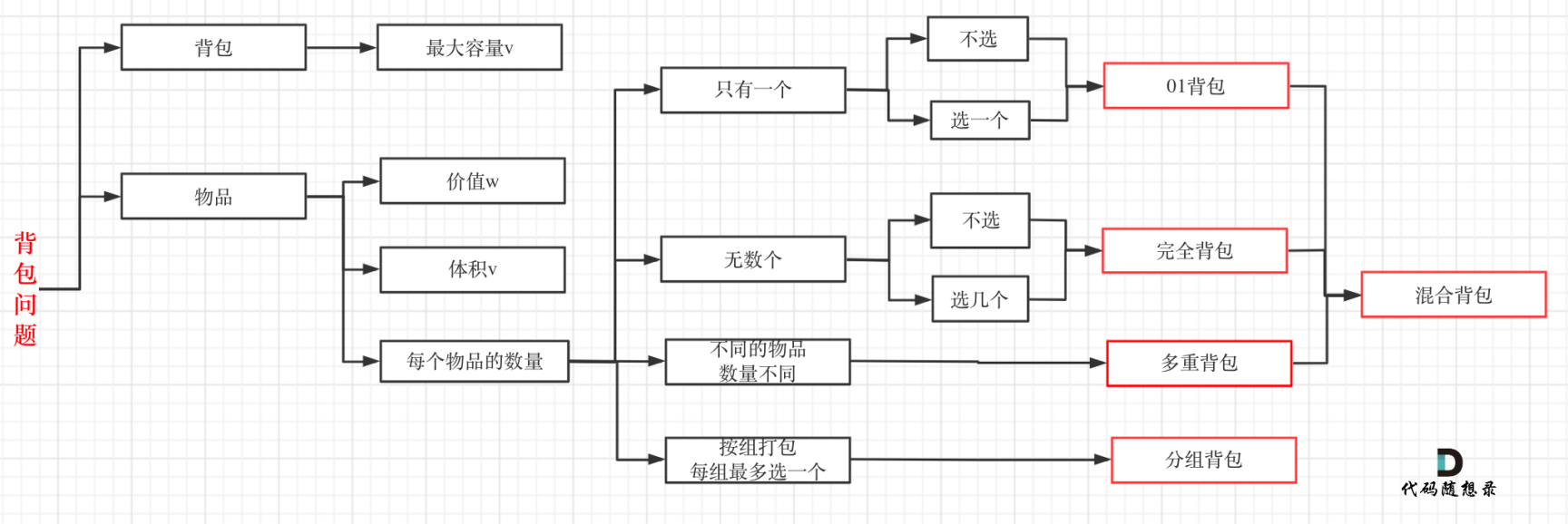
image-20210508233256021

背包问题是动态规划问题。

01背包

由上图可知，01背包的物品个数只有1，要么选，要么不选。

有N件物品和⼀个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能⽤⼀次，求解将哪些物品装⼊背包⾥物品价值总和最⼤。

如果通过暴力解法去解，则要将所有的情况列出来，即每个物品都有两种可能，取或不去。所以有2的n次方种情况，n代表物品的件数。

时间复杂度就是O(2^n)。

采用动态规划进行优化

二维数组

假设 背包最⼤重量为4，物品为：

重量 价值
物品0 1 15
物品1 3 20
物品2 4 30
  1. 确定dp数组以及下标的含义

定义dp[i][j] 表示从下标为 [0-i]的物品⾥任意取，放进容量为j的背包，价值总和最⼤是多少。

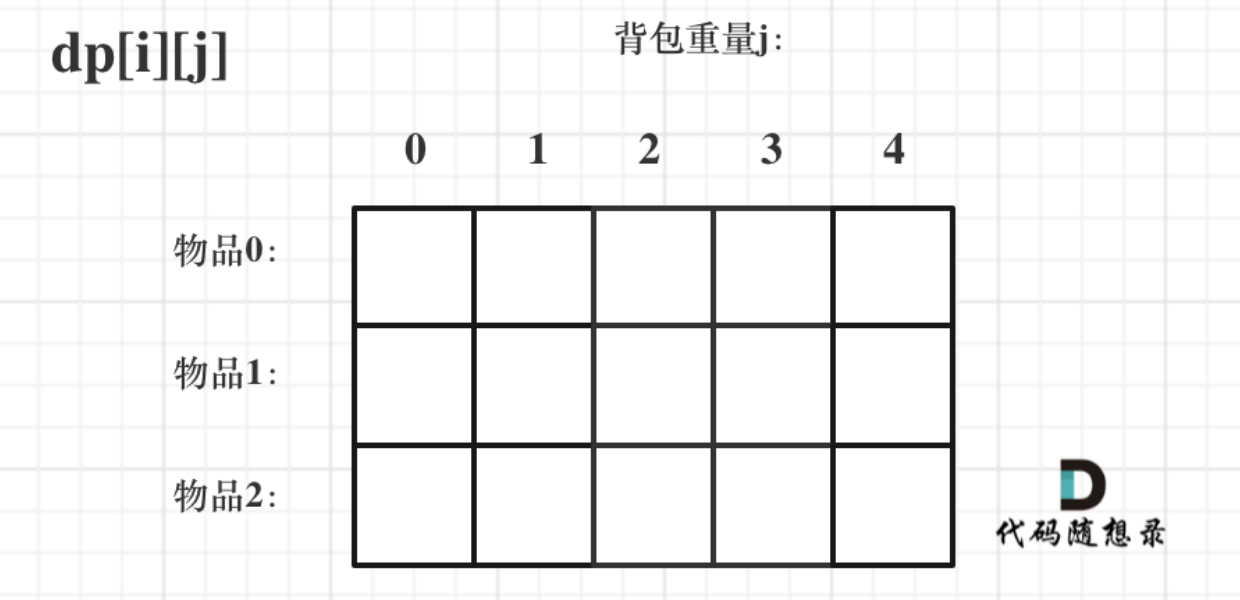
image-20210508234909469
  1. 确定递推公式

有两个⽅向推出来dp[i][j]

  • 不选择下标为i的物品 由dp[i - 1][j]推出， dp[i][j] = dp[i - 1][j]

  • 选择下标为i的物品 由dp[i - 1][j - weight[i]]推出 dp[i][j] = dp[i][j] = dp[i - 1][j - weight[i]] + value[i]

递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

  1. dp数组如何初始化

关于初始化，⼀定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

⾸先从dp[i][j]的定义触发，如果背包容量j为0的话，即dp[i][0]，⽆论是选取哪些物品，背包价值总和⼀定为0。如图：

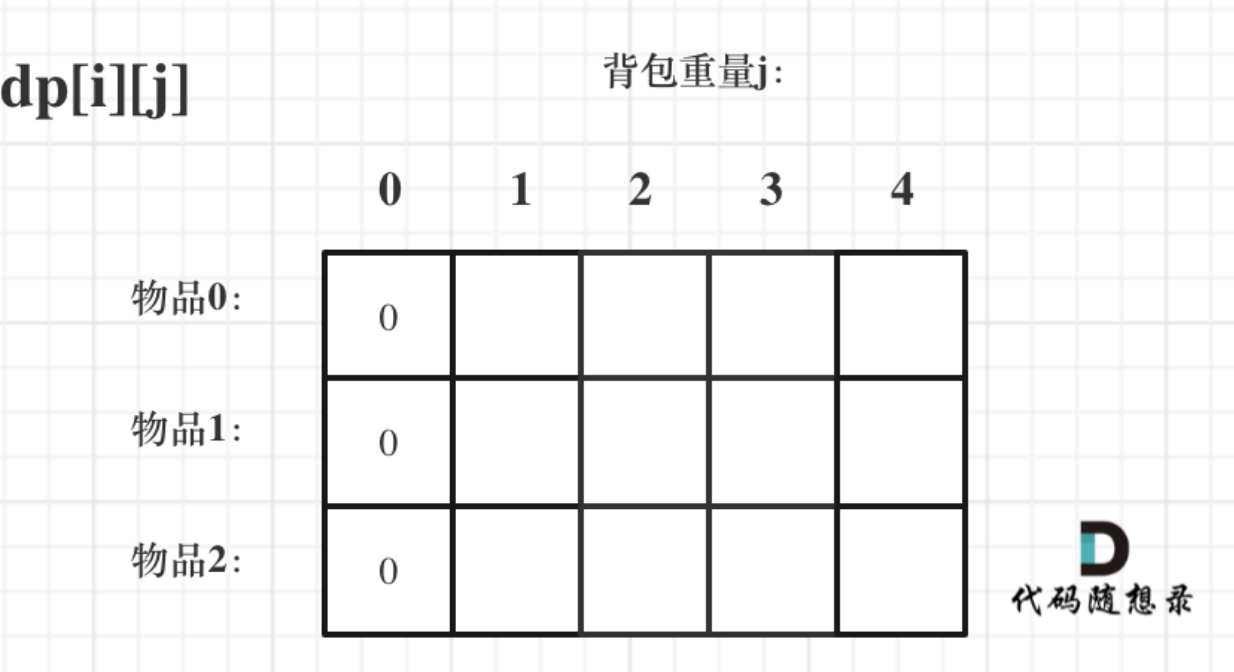
image-20210508235958966

i是由i-1推导的，当i为0时⼀定要初始化。

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最⼤价值。

1
2
3
4
5
6
7
8
// 倒叙遍历 保证物品被使用一次
for (int j = bagWeight; j >= weight[0]; j--) {
 dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i为0时候的情况
}
// 正序遍历 dp[0][j - weight[0]]中可能已经加了 value[0]
for (int j = weight[0]; j <= bagWeight; j++) {
 dp[0][j] = dp[0][j - weight[0]] + value[0];
}

dp数组初始化情况:

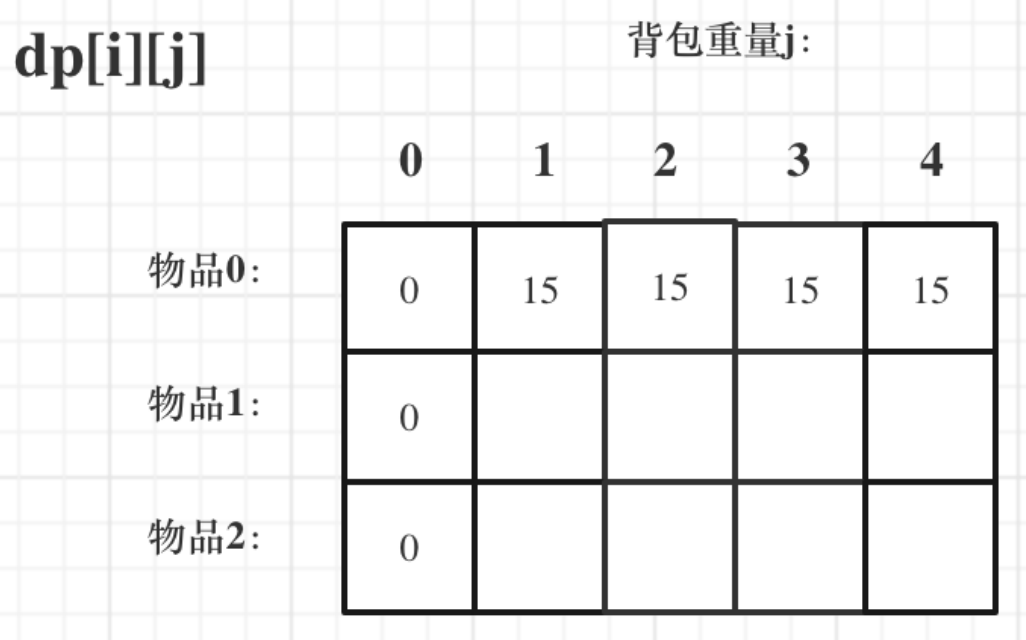
image-20210509000854888

其他下标应该初始化多少呢？dp[i][j]在推导的时候⼀定是取价值最⼤的数，如果题⽬给的价值都是正整数那么⾮0下标都初始化为0就

可以了，因为0就是最⼩的了，不会影响取最⼤价值的结果。如果题⽬给的价值有负数，那么⾮0下标就要初始化为负⽆穷了。

  1. 确定遍历顺序

可以看出，有两个遍历的维度：物品与背包重量。应该先遍历哪个？其实都可以！！ 但是先遍历物品更好理解。

1
2
3
4
5
6
7
8
// 先遍历物品
// weight数组的⼤⼩ 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
 for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
 if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 容量不够->不选
 else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
 }
}
1
2
3
4
5
6
7
8
// 先遍历背包重量
// weight数组的⼤⼩ 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
 for(int i = 1; i < weight.size(); i++) { // 遍历物品
 if (j < weight[i]) dp[i][j] = dp[i - 1][j];
 else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
 }
}
  1. 举例推导dp数组
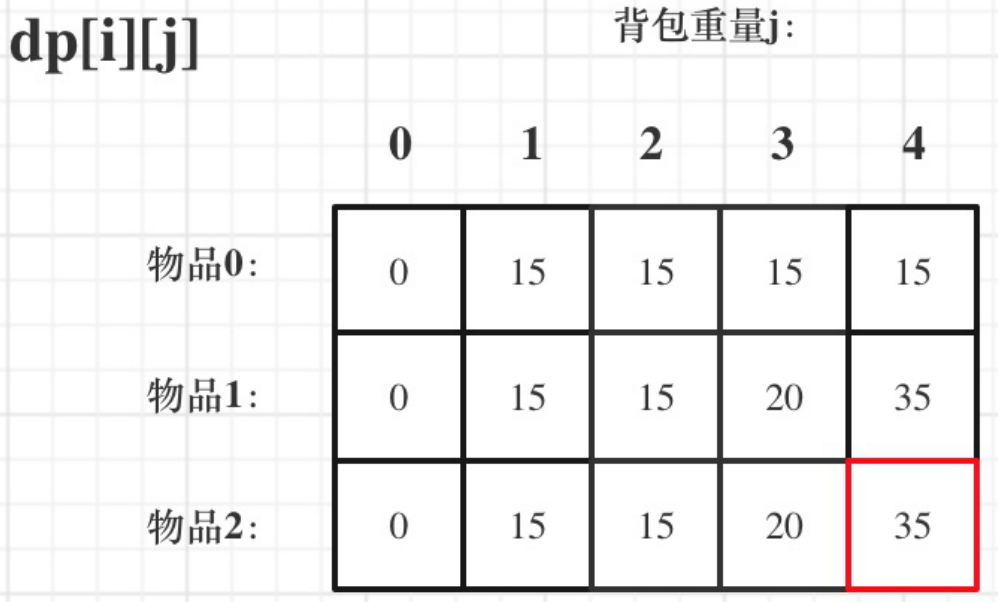
image-20210509002110466

最终结果就是dp[2][4]。

做动态规划的题⽬，最好的过程就是⾃⼰在纸上举⼀个例⼦把对应的dp数组的数值推导⼀下，然后在动⼿写代码！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func main() {
	var w = 4
	weight := []int{1, 3, 4}
	value := []int{15, 20, 30}

	dp := make([][]int, len(weight))
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]int, w+1)
	}

	//初始化
	for i := 0; i < len(weight); i++ {
		dp[i][0] = 0
	}
	for j := w; j >= weight[0]; j-- {
		dp[0][j] = dp[0][j-weight[0]] + value[0]
	}
	
	for i := 1; i < len(weight); i++ {
		for j := 0; j <= w; j++ {
			if weight[i] > j {
				dp[i][j] = dp[i-1][j]
			} else {
				dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
			}
		}
	}
	fmt.Println(dp[len(weight)-1][w])
}

func max(a, b int) int {
	if a >= b {
		return a
	}
	return b
}

一维数组(滚动数组)

对于背包问题其实状态都是可以压缩的。

在使⽤⼆维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]

如果把 dp[i - 1] 那⼀层拷⻉到 dp[i] 上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])

这样就可以用一维数组表示。这就是滚动数组的由来，需要满⾜的条件是上⼀层可以重复利⽤，直接拷⻉到当前层。

动规五部曲分析如下：

  1. 确定dp数组的定义

在⼀维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最⼤为dp[j]。

  1. ⼀维dp数组的递推公式

dp[j] 表示 容量为j的背包所背的最⼤价值，那么如何推导dp[j]呢？

dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最⼤价值。

此时dp[j]有两个选择，⼀个是取⾃⼰dp[j]，⼀个是取dp[j - weight[i]] + value[i]，这就要看谁大了。

所以递归公式为：

1
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  1. ⼀维dp数组如何初始化

关于初始化，⼀定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

dp[j]表示：容量为j的背包，所背的物品价值可以最⼤为dp[j]。

那么dp[0]就应该是0，因为背包容量为0,所背的物品的最⼤价值就是0。

其他下标初始化。根据题目要求选择合适的值。

  1. ⼀维dp数组遍历顺序
1
2
3
4
5
for(int i = 0; i < weight.size(); i++) { // 遍历物品
 for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
 	dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
 }
}

这⾥和⼆维dp的写法中，遍历背包的顺序是不⼀样的！

⼆维dp遍历的时候，背包容量是从⼩到⼤，⽽⼀维dp遍历的时候，背包是从⼤到⼩。

⼀维dp数组的背包在遍历顺序上和⼆维其实是有很⼤差异的！，这⼀点⼀定要注意。

  1. 举例推导dp数组
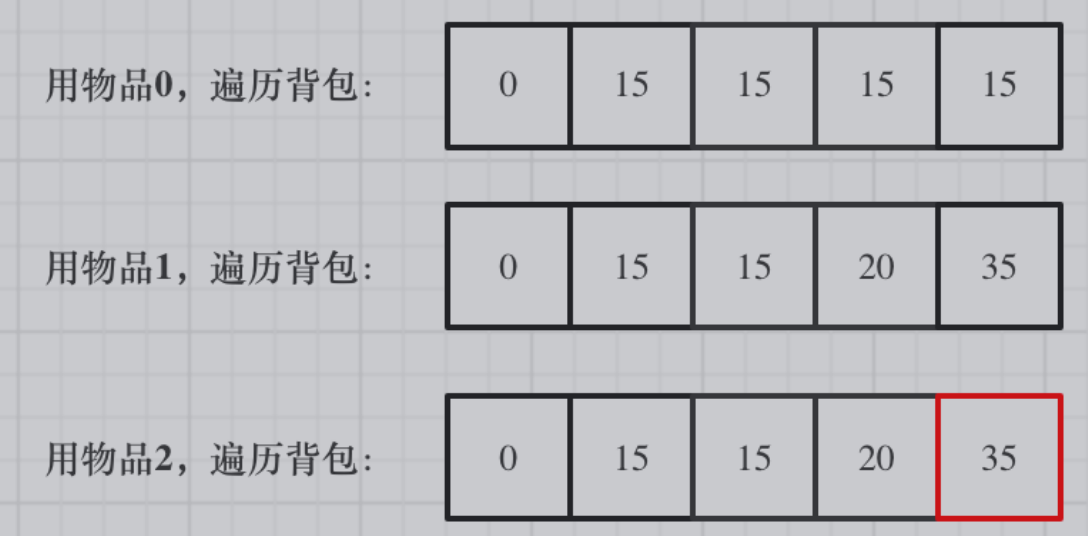
image-20210509004924306

⼀维dp 的01背包，要⽐⼆维简洁的多！ 初始化 和 遍历顺序相对简单了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func main() {
	var w = 4
	weight := []int{1, 3, 4}
	value := []int{15, 20, 30}

	dp := make([]int, w+1)

	//初始化 dp[0]=0

	for i := 0; i < len(weight); i++ {
		for j := w; j >= weight[i]; j-- {
			dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
		}
	}
	fmt.Println(dp[w])
}

func max(a, b int) int {
	if a >= b {
		return a
	}
	return b
}

例题

  1. 分割等和⼦集

只要找到集合⾥能够出现 sum / 2 的⼦集总和，就算是可以分割成两个相同元素和⼦集了。

转换为背包问题

根据题目设定可知：

  • 背包的体积w为sum / 2 且不大于10000
  • 背包要放⼊的商品（集合⾥的元素）重量为 元素的数值，价值也为元素的数值 , 即 nums=weight=value
  • 背包正好装满，说明找到了总和为w 的⼦集。即dp[w] == w （前提 num%2==0）
  • 背包中每⼀个元素是不可重复放⼊。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func canPartition(nums []int) bool {
  sum := 0
	for _, num := range nums {
		sum += num
	}
	// 如果是奇数 肯定不会相等
	if sum%2 == 1 {
		return false
	}

	w := sum / 2
	dp := make([]int, w+1)

	for i := 0; i < len(nums); i++ {
		for j := w; j >= nums[i]; j-- {
			dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])
		}
	}
	if dp[w] == w {
		return true
	}
	return false
}

func max(a, b int) int {
	if a >= b {
		return a
	}
	return b
}
  1. 最后⼀块⽯头的重量 II

本题其实就是尽量让⽯头分成重量相同的两堆，相撞之后剩下的⽯头最⼩，与上题类似，在最后的处理上有所不同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func lastStoneWeightII(stones []int) int {
  sum := 0
	for _, num := range stones {
		sum += num
	}

	w := sum / 2
	dp := make([]int, w+1)

	for i := 0; i < len(stones); i++ {
		for j := w; j >= stones[i]; j-- {
			dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
		}
	}
	// dp[w] <= w
	return sum - dp[w] - dp[w]
}

func max(a, b int) int {
	if a >= b {
		return a
	}
	return b
}

完全背包

完全背包和01背包问题唯⼀不同的地⽅就是，每种物品有⽆限件。

01背包和完全背包唯⼀不同就是体现在遍历顺序上，所以直接针对遍历顺序经⾏分析！

我们知道01背包内嵌的循环是从⼤到⼩遍历，为了保证每个物品仅被添加⼀次。

⽽完全背包的物品是可以添加多次的，所以要从⼩到⼤去遍历，即：

1
2
3
4
5
6
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
	for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量
		dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
 	}
}
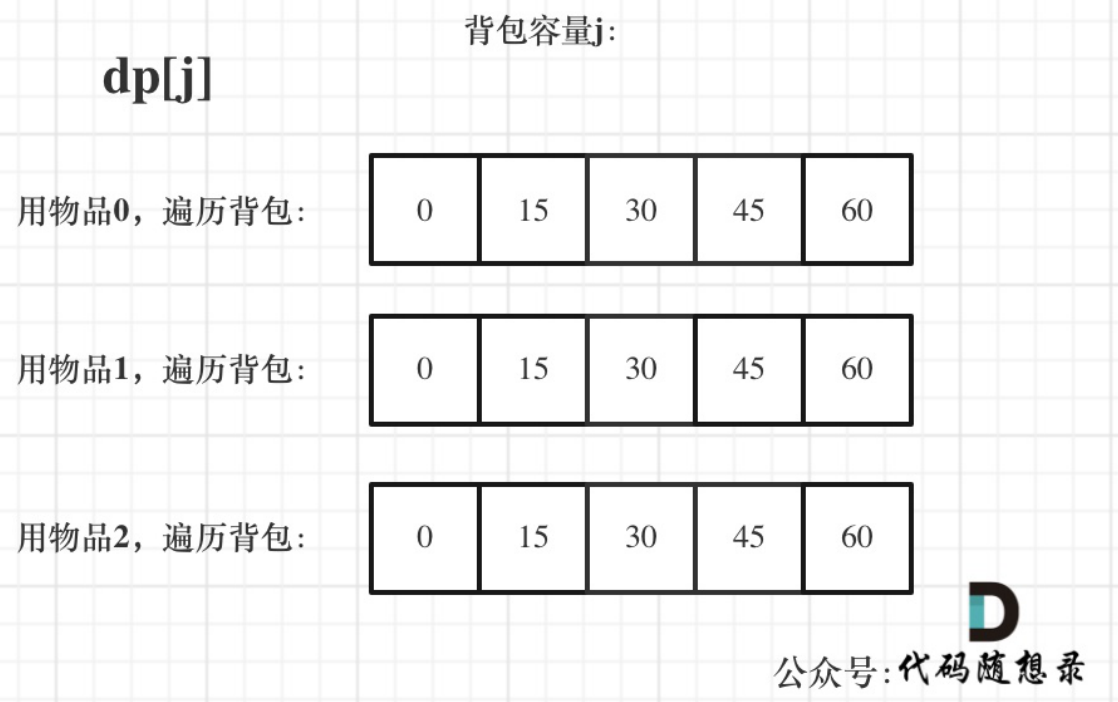
image-20210509113830415

为什么遍历物品在外层循环，遍历背包容量在内层循环？

01背包中

  • ⼆维dp数组的两个for遍历的先后循序是可以颠倒的
  • ⼀维dp数组的两个for循环先后循序⼀定是先遍历物品，再遍历背包容量。

在完全背包中，

  • 对于⼀维dp数组来说，其实两个for循环嵌套顺序同样⽆所谓！

因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 一维数组
func main() {
	var w = 4
	weight := []int{1, 3, 4}
	value := []int{15, 20, 30}

	dp := make([]int, w+1)

	for i := 0; i < len(weight); i++ {
		for j := weight[i]; j <= w; j++ {
			dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
		}
	}
	fmt.Println(dp[w])
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 二维数组
func main() {
	var w = 4
	weight := []int{1, 3, 4}
	value := []int{15, 20, 30}

	dp := make([][]int, len(weight))
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]int, w+1)
	}

	//初始化
	for i := 0; i < len(weight); i++ {
		dp[i][0] = 0
	}
	// 正序
	for j := weight[0]; j <= w; j++ {
		dp[0][j] = j / weight[0] * value[0]
	}

	for i := 1; i < len(weight); i++ {
		for j := 0; j <= w; j++ {
			if j < weight[i] {
				dp[i][j] = dp[i-1][j]
			} else {
				dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
			}
		}
	}
	fmt.Println(dp[len(weight)-1][w])
	fmt.Println(dp)
}

例题

  1. 零钱兑换 II

本题和纯完全背包不⼀样，纯完全背包是能否凑成总⾦额，⽽本题是要求凑成总⾦额的个数！

注意题⽬描述中是凑成总⾦额的硬币组合数

求组合数还是排列数 会影响遍历的顺序

动态规划五部曲:

  1. 确定dp数组以及下标的含义

    dp[j]：凑成总⾦额j的货币组合数为dp[j]

  2. 确定递推公式

由原来组合方式的基础上 加上 加入当前硬币后新增的方式

dp[j] = dp[j] + dp[j - coins[i]]

  1. dp数组如何初始化

⾸先dp[0]⼀定要为1，dp[0] = 1的含义是凑成总⾦额0的货币组合数为1。

  1. 确定遍历顺序

本题中是外层for循环遍历物品（钱币），内层for遍历背包（⾦钱总额），还是外层for遍历背包（⾦钱总额），内层for循环遍历物品（钱币）呢？

上文讲过完全背包的两个for循环的先后顺序都是可以，但本题就不⾏了！

因为纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也⾏，没有顺序也⾏！

⽽本题要求凑成总和的组合数，元素之间要求没有顺序。

如果先遍历物品再遍历容量，那么是在第一个物品遍历完后，再遍历另一种物品。这样能保证顺序是固定的(求组合)。

如果先遍历容量在遍历物品，那么顺序是不确定的(求排列)。

建议动⼿把这两种⽅案的dp数组数值变化打印出来，对⽐看⼀看！（实践出真知）

  1. 举例推导dp数组

输⼊: amount = 5, coins = [1, 2, 5] ，dp状态图如下：

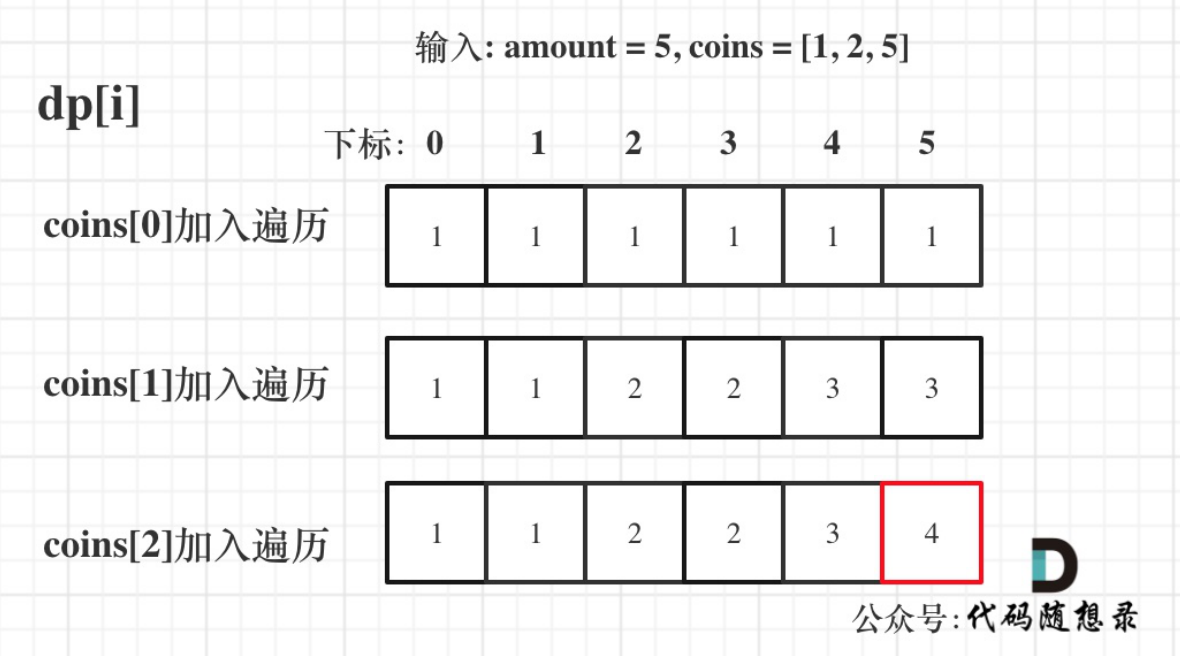
image-20210509214749962 
1
2
3
4
5
6
7
8
9
10
11
12
13
func change(amount int, coins []int) int {
    // dp[i] 表示 金额为i时 一共有几种组合方式
    dp := make([]int, amount+1)
    dp[0] = 1
    // 组合 --> 要先遍历物品再遍历容量
    for i:=0; i<len(coins); i++ {
        for j:=coins[i]; j<=amount; j++ {
            // 原来的组合方式数 + 加入该枚硬币后新增的组合数
            dp[j] = dp[j] + dp[j-coins[i]] 
        }
    }
    return dp[amount]
}

多重背包

多重背包与01背包和完全背包的区别在于，物品的是一个特定的值。

假如物品A的数量是2，把物品A当做两个独立的物品，那数量都是1，那么就转化为01背包问题了。

时间复杂度：O(m * n * k) m：物品种类个数，n背包容量，k单类物品数量

  1. 构建一个新的weight数组和value数组

  2. 直接在2层for循环中再加一个循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func main() {
	var w = 10
	weight := []int{1, 3, 4}
	value := []int{15, 20, 30}
	nums := []int{2, 3, 2}

	dp := make([]int, w+1)

	//初始化 dp[0]=0

	for i := 0; i < len(weight); i++ {
		for j := w; j >= weight[i]; j-- {
			// 以上为01背包，然后加⼀个遍历个数
			for k := 1; k <= nums[i] && (j-k*weight[i]) >= 0; k++ { //遍历个数
				dp[j] = max(dp[j], dp[j-k*weight[i]]+k*value[i])
			}
		}
		fmt.Println(dp)
	}
	//fmt.Println(dp)
}
  1. 还有那种⼆进制优化的⽅法，其实就是把每种物品的数量，打包成⼀个个独⽴的包。
Donate comment here.